The shelf life of a product is a length of time an SKU can be stored on shelf without becoming unfit for use. Retailers commonly use the strategy of “Stock Rotation and Rationalization” — moving the SKU’s with the earliest sell dates so that shoppers pick them before the expiration date without any loss to the retailer.

Sometimes it becomes necessary to sell the slow-moving SKU’s with a shorter shelf life at a lower price point to increase the velocity of SKU.

When a SKU/Product Line is sold at a lower price point or a discounted price, it results in a Marginal Loss to the retailer. For retailers, coming up with maximum possible discount without incurring a Marginal Loss is a challenge.

Infogain’s Analytical Approach

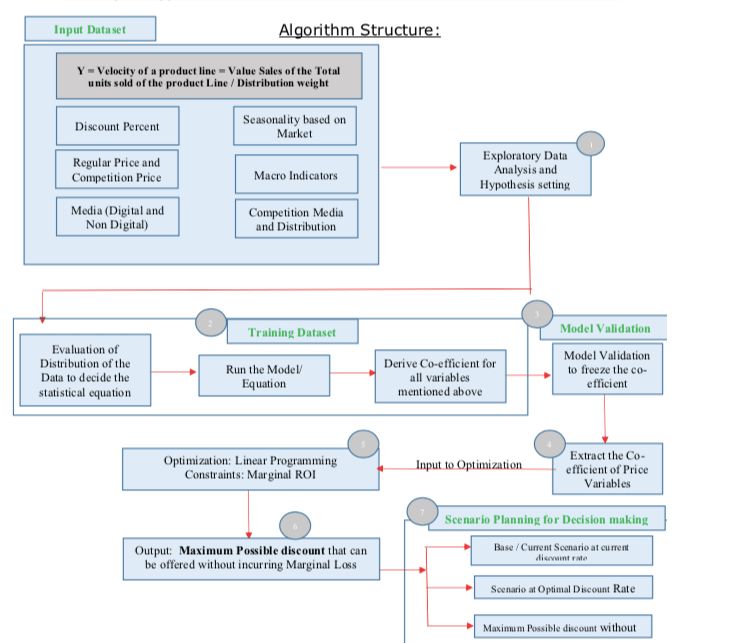
Co-efficient Estimate for price variables

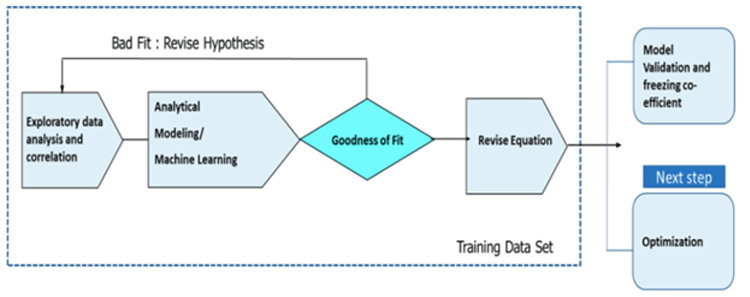
(Co-efficient = Delta Y / Delta X) Step 1: Co-efficient Estimation
Based on the distribution of the data, the appropriate Statistical Equation is applied to the data to estimate the co-efficient of price Variables.:

Y = Velocity of a Product Line of perishable Product Line/List of SKU

1. X1 = Discounted Price (Percent)
2. X2 = Relative Regular Price Index (Our price / Competition regular Price) +
3. X3 = Digital Media+
4. X4 = Seasonality
5. X5 = Non-Digital Media
6. X6 = Competition Media
7. X7 = Any Other Macro / Micro Factors

Key Factors of the Co-Efficient Price Equation

• The Non–Price variable data will help in estimating the co-efficient of Price Variables accurately.
  If Non–Price data is not available; the equation will be run with price variables alone.
• The contribution to revenue other than price will be attributed to Base.
• In order to accurately simulate a scenario with an optimal discount without any marginal loss, it is critical to measure the influence of all factors (including competition and media). Based on the category and market, seasonality could be removed from the data if it is not provided.

Infogain’s Price Optimization to estimate Optimal Discount

Infogain’s Algorithm uses the co-efficient obtained from the co-efficient estimate for price variables equation, running Optimization to arrive at an optimal discount price point based on Marginal ROI Analysis:

• Marginal ROI at a time (t2) = Delta Total Value Sales (t2-t1) / Delta Total Cost (t2-t1)
• Total Revenue at a time (t) = Total Units sold at a time (t) * Selling Price at time (t)
• Total Cost = Total Units Sold * Marginal Cost.
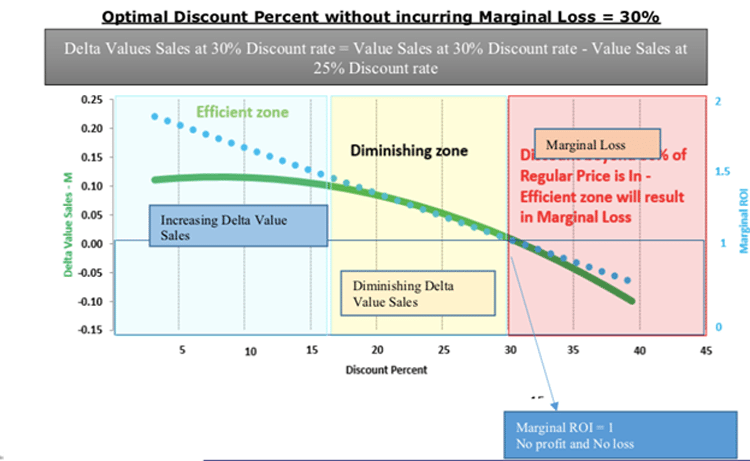
  Marginal Cost = Cost of producing one additional unit of product
• Delta value sales = Values sales at 30% discount rate minus value sales at 25% discount rate

Although the Volume Sales will go up with the increased discount, Value Sales won’t necessarily go up as well.

Infogain’s Optimization Approach Illustrated

Optimization: Mathematical Linear Programming and Optimization

Objective Function: Minimize the Delta Value Sales

Variable: Discount Percent

Constraint: Marginal ROI should be equal to 1

Optimal Discount Percent based on Marginal ROI Analysis = Discount percent 15%
Discount Percent Point without incurring Marginal loss = 30%
Any Discount beyond 30% will lead to Marginal loss

Infogain’s Value Addition—Scenario Planning for data driven decision making

1. BASE SCENARIO:

What is the base /current scenario? Marginal cost and profit evaluation of current Situation

(Are you currently below optimal Discount or above Optimal Discount or incurring loss? Or is there any scope of improvement)

1. SCENARIO WITH OPTIMAL DISCOUNT RATE:

What is the Optimal Discount Rate? (15 % as seen above)

3. MAXIMUM DISCOUNT RATE WITHOUT INCURRING MARGINAL LOSS:

What is the highest possible discount rate that can be offered without incurring marginal loss? (Ex. Scope to increase discount rate up to 30% as seen above)

Assumptions and Complexities

1. According to the Managerial Microeconomic price-demand theory, price and demand always has an inverse relationship. With a decrease in regular price (increase in discount rate) an increase in demand is observed.

This relationship is mostly linear in nature.  Infogain has suggested Linear Programing for optimization based on the Domain experience, managerial economic price demand function theory and APAC Market Knowledge. If we don’t see a linear relationship between price and demand, however, an appropriate non –linear programming will be applied for Optimization and statistical equation based on trend observed in the data.

1. Seasonality factor can be extrapolated by Infogain if not provided.

3. Assumption is made that media and competition data will be available to estimate co- efficient of price accurately

Conclusion

The Marginal ROI Model is used for solving many computational financial problems ranging from Option Pricing to investment decisions such as cost minimization and profit maximization. Several Marketing and Consumer Packaged Goods (CPG) companies have adopted the Marginal ROI Analysis for best pricing in order to achieve Maximize Profitability.

Linear programming Marginal ROI Model can help retailers select the best possible discount strategy for perishable goods without incurring any marginal loss . The Scenario planner can help them evaluate the marginal cost vs profit of various discount alternatives. The Model can also help retailers forecast profitability for future.

To learn more about the Infogain’s  Linear programming Marginal ROI Model, contact analytics@infogain.com.

About Infogain

Infogain is a global business-oriented IT consulting provider of front-end, customer-facing technologies, processes and applications, leading to a more efficient and streamlined customer experience. We want our clients’ interactions with their customers to be fast, efficient, and cost effective.

With close to 4,000 employees in the United States, India, the Middle East, U.K., Singapore and Malaysia, we service 5 of the world’s largest 50 companies, and 24 of the Fortune 500. we have million-dollar engagements with over 25 customers, many of which have been with us for 5 years or more.